Learning from experience and making predictions that will guide future actions are at the core of intelligence. These tasks need to embrace uncertainty to avoid the risk of drawing wrong conclusions or making bad decisions. The sources of uncertainty are manifold ranging from measurement noise, missing information, and insufficient data to uncertainty about good parameter values or the adequacy of a model. Probability theory offers a framework to represent uncertainty in the form of probabilistic models. The rules of probability theory allow us to manipulate and integrate uncertain evidence in a consistent manner. Based on these rules, we can make inferences about the world in the context of a given model. In this sense, probability theory can be viewed as an extended logic.

Probabilistic models and inference

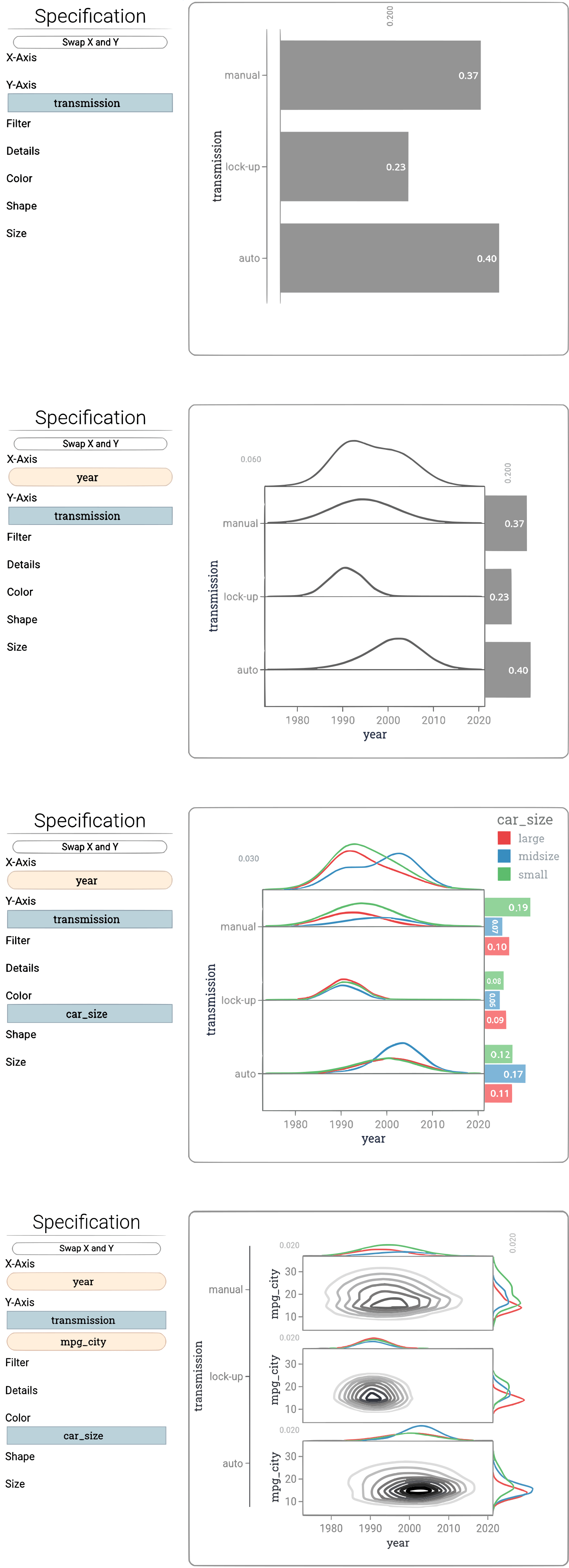
A probabilistic model is a representation of possible data that could be observed. It can be given in functional form such as a multivariate Gaussian or a mixture model, or, more generally, in the form of a process or probabilistic program. A model can be used to inform our decision-making in the light of partial evidence. Good and robust decisions should take into account all the relevant uncertainty, which is the purpose of probabilistic expert systems. For example, a simple system could involve only two statements, "the sky is cloudy" and "the grass is wet", both of which can either be true or false. Our expert system is based on the probabilities of each of the four possible scenarios ("sky is cloudy and grass is wet", etc.). The partial evidence "the sky is cloudy" changes our belief whether the grass is wet. To do the inference, we compute the conditional probability of the statement "the grass is wet", which will generally be different from our judgment ignoring observations of the sky (expressed by a marginal probability). A visualization of a sequence of inference queries on a more complex model of car fuel efficiency can be seen on the right.

In the example, the probabilities used by the system do not change. However, we might also want to update our model based on new evidence. This is one of the major tasks in Bayesian inference. Again, we need to compute conditional and marginal probabilities that will now inform us about plausible parameter values or allow us to compare alternative models. The computational challenges that we face in probabilistic inference are the same no matter whether we follow a Bayesian approach or not. In both scenarios, we need to compute marginals, conditionals and aggregations like the maxima of distributions. For many models of interest, exact inference is intractable because it scales exponentially with the number of variables.

Algorithmic challenges

The algorithmic challenges of probabilistic inference are far from being solved and often become a bottleneck for probabilistic modeling and inference. Although probabilistic programming languages automate inference of models at various degrees of sophistication, the generic inferences of these languages are often outperformed by customized inference techniques. As of today, general-purpose inference remains very challenging. Here, we address these challenges by means of enabling technologies including algorithm engineering, high-performance computing, automatic differentiation, logic, and visualization.

Funding Details

The Interactive Inference Project is funded by the Carl-Zeiss-Stiftung within the program Scientific Breakthroughs in Artificial Intelligence from April 2022 to March 2028. Funding budget: 4.905.000 Euro

Newsletter Subscription

For regular updates on our upcoming events and seminars, please subscribe to our newsletter.